Although radial distances will be given from the black hole in both Schwarzschild radii (R_S) and kilometers (km), please note that one cannot simply measure this distance with a series of meter sticks. This is because, for one reason, any meter stick closer than the event horizon could not be seen by an observer outside the event horizon. A better way of visualizing radial distance is to picture orbiting the black hole at a fixed distance, measuring the circumference of the orbit, and dividing by 2 pi.

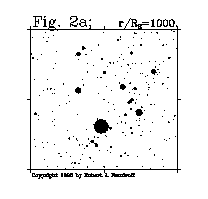
Far from the black hole an undistorted night sky is visible with a very small patch of fuzz in the center. As the viewer nears the black hole the fuzzy patch becomes discernable as an unusual conglomeration of stellar images. Fig. 2a depicts the view visible from 1000 R_S (4200 km) away.
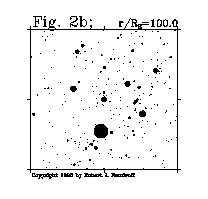
Fig. 2b shows the black hole from a distance of 100 R_S (420 km). From this distance the viewer begins to notice that no light comes from a circular patch in the direction of the black hole. The only light that could possible come to the viewer from this area would be from the black hole itself. Since here it is considered that the black hole emits no light [28], this area is dark. The angular size of the filled black circle is the angular size of the photon sphere of the black hole mass and can be found from the discussion in the Appendix.

Fig. 2c shows the black hole from a distance of 25 R_S (105 km). Here the angular size of the black hole has increased and the secondary images, which are inside the first sky Einstein ring, are now quite clearly discernable.

Fig. 2d shows the black hole from a distance of 10 R_S (42.0 km). Here the viewer should notice that the placements of stellar images near the black hole have changed greatly when compared to Fig. 2a. Stars nearest to behind the black hole from the observer now have two bright images. The brightest star in the illustration (and the sky: Sirius) can be seen to have two bright images: the brightest primary image in the field of view on the lower left and a secondary image 180 degrees across the face of the black hole from it. Primary and secondary images can always be matched up by connecting them with a Great Circle (a line on these figures) through the center of the black hole. Sirius is not the only star to have two distinct images, however. Notice that Betelgeuse and each star in the belt of Orion also has two bright images. Sirius and the stars in the belt of Orion have been labelled in Fig. 2d. In fact, all bright stars visible in the field have two bright images. Some dim stars that previously could not be seen now have been amplified by the gravitation of the black hole to exhibit observably bright images. In Fig. 2d, the first sky Einstein ring has been drawn in with a dashed line.
The first sky Einstein ring, shown in Fig. 2d, is an invisible circle centered on the black hole and dividing the first complete set of images (those angularly furthest from the disk of the black hole which lie between the zeroth and first Einstein rings) from the second complete set of images. Each image in the first set is always brighter than the corresponding image in the second set. The second sky Einstein ring appears in the conglomeration of stellar images near the apparent photon sphere position, just outside the photon sphere. A complete image of the sky can be seen between these two Einstein rings.
Note that typically stellar images get much dimmer as one looks closer to the apparent photon sphere position, but the average surface brightness of the sky there remains unchanged. In other words, if Fig. 2d was spun about the center of the black hole smearing all the star images into a blur, the inner regions near the apparent position of the photon sphere would appear to have the same average brightness as the outer regions near the edge of the illustration. This is a consequence of conservation of surface brightness discussed above.






The viewer now does an orbit around the black hole at the radius of 10 R_S (42 km). The distortions the viewer would see are shown in Figs. 2d - 2j. These figures depict viewing angles for relative angular positions of 0 degrees, 5 degrees, 10 degrees, 90 degrees, 180 degrees, 270 degrees, and 360 degrees around the orbit. A complete orbit would encompass, of course, 360 degrees and so Fig. 2j is the same as Fig. 2d.
Fig. 2e, showing a relative 5 degrees orbital angle compared to Fig. 2d, has several interesting differences with this figure. Stellar images nearest the first sky Einstein ring have shifted the most. These images represent stars that are closest to directly behind the black hole from the viewer. These images appear to move with the highest angular speeds. This is because a small angular (unlensed) step of the star from just to the left of behind the black hole from the observer to just to the right causes all of its images to move from one side of the Einstein ring to the other. Apparent angular speeds have no maximum limit. If one attributes a distance to the images they can even appear to exceed the speed of light. Note that images of the same star still appear 180 degrees across the face of the black hole from each other, and that the brighter image is outside the first Einstein ring, while the dimmer image is inside.
Remember, an entire single image of the sky is contained between the zeroth and first sky Einstein rings. It is therefore impossible for an image to leave this region - it cannot just "go" across this ring and end up between the first and second Einstein rings. Stars (in reality) approaching the nadir point below the black hole from the viewer (moving slowly) have images that appear to approach the Einstein ring and get very bright (moving rapidly), eventually receding from this Einstein ring and dimming.
After a complete orbit with the viewer always facing the black hole, the distortions are depicted by Fig. 2j, which is the same as Fig. 2d. This figure is included to provide continuity in the presented sequence.

Now the viewer will go even closer to the black hole. Fig. 2k shows the visible distortions from 3 R_S (12.6 km): at twice the distance of the photon sphere. Here the viewer is looking 45 degrees away from the black hole. Note the great number of clearly resolved secondary images visible near the black hole's limb.

The viewer now reaches the photon sphere and looks up from the black hole to peer directly along the photon sphere. Fig. 2l shows the distortions from this distance: 1.5 R_S (6.3 km). The viewer looks north. The self Einstein ring where viewers could see the backs of their heads is the photon sphere horizon line dividing the light captured by the black hole from the the light coming from the sky: it is a horizontal line across the middle of the figure. The first sky Einstein ring would be an invisible line about 2/9 of the way toward the top of the plot above the photon sphere. Since the viewer's location and orientation does not allow the whole face of the black hole to be visible, both of the bright images (the primary and secondary image) of a single star are not visible at the same time. Those stellar images highly amplified above the Einstein ring are different than those that appear highly amplified just below the Einstein ring. The primary images just above the Einstein ring in one direction will have their secondary image appear just below the Einstein ring in the opposite direction.


The viewer now starts along an orbit at the photon sphere, 1.5 R_S (6.3 km) from the black hole. The position of the first sky Einstein ring becomes more evident when comparing Figs. 2l, 2m, and 2n which have relative orbital angles of 5 degrees and 10 degrees.
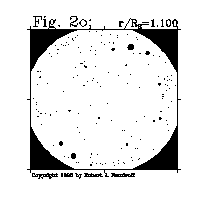
The viewer now descends and looks directly away from the black hole. Fig. 2o shows the distortions from 1.1 R_S (4.62 km). All of the sky images are now compressed into a hole in the direction opposite the black hole.

Fig. 2p shows the distortions visible from 1.01 R_S (4.242 km) while looking directly away from the black hole. The black hole now encompasses almost the complete observer sky. The small hole at the top is what remains visible of the outside universe. In this hole there could appear, theoretically, an infinite number of complete images of the outside universe. The angular amplification A_angular of the vast majority of these images is, however, much less than unity: they are greatly deamplified.
Fig. 2p, as shown, is not an accurate depiction of the distortions a viewer would see in this position. It is included because part of it is correct and the part that is not is informative. The part that is correct is the depiction of the relative amounts of black hole and background sky that are visible. The thin fuzzy annular ring is not realistic, however, as the program plotted mostly just the positions of the secondary images. Only a handful of primary sky images are visible as most of them have suffered large angular deamplifications. As stated above, the secondary images are plotted by the program regardless of the amount of deamplification. The outer radial limit of the dim ring marks the position of the second sky Einstein ring. Stellar images that would be seen between there and the apparent photon sphere limb of the black hole would be even higher order images. This is the only figure where these images are noticeable by their absence. The programs were not set up to track these higher order images, and so they are not shown.