It is not necessary to specify a mass of the star for a description of a trip to it. All distances can be given in terms of the Schwarzschild radius of the star, and hence are all scalable by this factor. Distances will therefore be given first in terms of the number of Schwarzschild radii, and second, in parenthesis, in terms of kilometers for a specific model. For each star, the specific model used will be for a star of mass 1.4 M_sun. By the simple formula R_S = 2GM/c^2 = 3 km M/M_sun, this mass corresponds to a Schwarzschild radius of 4.2 km. The surface of this neutron star will be R_* = 3 R_S = 12.6 km.

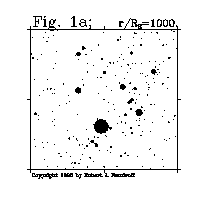
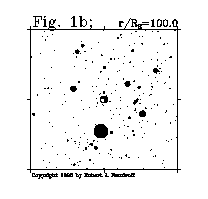
As the voyage starts, the viewer is moving through space toward the constellation Orion and the neutron star. At a distance from the neutron star of about 1000 R_S (4200 km), the neutron star destination comes into view. It is first noticeable as a very small fuzzy patch, as depicted in center of Fig. 1a. At 100 R_S (420 km) from the neutron star as depicted in Fig. 1b, the neutron star itself becomes visible and the fuzziness around it becomes resolved into a large conglomeration of individual secondary stellar images. Here for the first time the viewer can see detail inside the first sky Einstein ring. (To reiterate, Einstein rings are themselves usually invisible - they can be thought of as imaginary dividing lines between image sets.) This image conglomeration will have the same average surface brightness as the rest of the sky: if one could distribute the starlight in the rest of the sky about the whole sky it would appear to have the same apparent brightness.

As the viewer approaches the neutron star it becomes evident that stars that would have appeared eclipsed behind the neutron star in the absence of its gravitational field now appear to have two bright images: one just outside the first sky Einstein ring and one just inside. This is depicted in Fig. 1c where the viewer is now 25 R_S (105 km) from the center of the neutron star, 12.4 R_S (52.08 km) from its surface.

The viewer now descends to only 10 R_S (42 km) from the star's center. Visual distortions appear as in Fig. 1d. Many of the stellar images interior to the first sky Einstein ring can be very clearly resolved. No other Einstein rings are in the field of view. At this distance from the neutron star surface features can now be clearly resolved. Surface distortions can be highlighted by comparing the figure to a standard globe of the earth. More than half of the surface is visible here - but not the entire surface.
For clarity, the first sky Einstein ring has been drawn in with a dashed line in Fig. 1d. Also labels pointing out both the primary and secondary image of the belt of Orion are shown, as well as labels pointing out both the primary and secondary image of Sirius.






The viewer has now stopped at 10 R_S (42 km) and begins a circular orbit of the star. Figs. 1e-1j show views at relative orbital angles of 5, 10, 90, 180, 270, and 360 to the original viewer position. Fig. 1j is the same as Fig. 1d but is included to provide continuity in the presented sequence. It is particularly illuminating to compare Figs. 1d, 1e, and 1f. There the viewer can most clearly see the position of the first sky Einstein ring by the effect of the viewer's slight motion.
Note that although all stars in the sky have at least one image (the primary image between the zeroth and first sky Einstein ring), not all stars have two images. This is because the neutron star is not compact enough to allow a second sky Einstein ring at the present observer location. Therefore the whole sky image between the first and second sky Einstein rings is not entirely visible.
Background stars that would have appeared blocked by the neutron star in the absence of high gravity now appear greatly amplified and positioned near the first sky Einstein ring. These stars now have two bright images that appear on opposite sides of the face of the neutron star. When the observer is in orbit about the neutron star, stellar images outside the first sky Einstein ring still appear to revolve (due to the viewer's motion) in the same general sense as they would in the absence of gravity. Now, however, many of them have a secondary image visible inside the first sky Einstein ring. These images, by conservation of angular momentum, must remain in the plane defined by the source, observer, and lens center, but on the opposite side of the neutron star from the first image. Therefore these images, although rotating in the same sense (clockwise or counter-clockwise) as the first images, appear to counter-rotate around the neutron star center when compared to the stellar images just across the first sky Einstein ring from them.
The hypothetical point on the sky directly opposite the observer through the lens center has been transformed into a series of circles, the most prominent of which is the frequently discussed first sky Einstein ring. A stellar image can never be seen to cross a sky Einstein ring. For example, a single stellar image cannot move from the first complete sky image to the second complete sky image. When a star approaches this point, it will either pass above or below it. If it passes above, the primary image will appear to become greatly amplified and pass above the first sky Einstein ring. If it passes below, then the primary image will appear to become greatly amplified and pass below the first sky Einstein ring. Stars that would have been seen to approach this point in the absence of strong gravity now have images that are seen to approach the circle in the presence of strong gravity.
The description of the apparent motions of surface features are quite similar to those of the sky features. The first surface Einstein ring is not available, however, and so a complete image of the surface is not in view. It is possible, then, for some surface features to completely disappear from view. Notice that surface features that appear near the limb of the star are somewhat distorted. Surface features will not appear dimmer near the limb. This is a consequence of the conservation of surface brightness.

The viewer now begins to land on the neutron star. Fig. 1k shows the distortions from 8 R_S (33.6 km) and a viewing angle of 15 degrees from looking directly at the neutron star. The next figures is sequence, Figs. 1l, 1m, 1n, 1o, and 1p, show the distortions from distances of 7 R_S (29.4 km), 6 R_S (25.2 km), 5 R_S (21 km), 4 R_S (16.8 km), and 3 R_S (12.6 km) while the viewing angle pans up from the star to angles 30 degrees, 45 degrees, 60 degrees, 75 degrees, and 90 degrees respectively.





Fig. 1p depicts the distortions a viewer would see from the neutron star surface looking directly tangent to the surface (90 degrees from looking directly at the neutron star). From the surface one can no longer see any sky Einstein rings and hence no secondary images of background stars.